機械学習 基礎の基礎 – scikit learn使って最小二乗法で回帰 –
はじめに
以前の記事、機械学習とかDeep Learningを学ぶ前に知っておくべき基礎の基礎では、
機械学習や深層学習を学ぶ前に、概要や基本的な用語について説明しました。
今回はもう少し具体的に、機械学習の分析手法についてご紹介します。
環境
今回使用した動作環境は以下のとおりです。
- OS : MacOS X 10.14.5
- python : 3.6.7
回帰
機械学習を学ぼうとしたとき、おそらく最初に登場するのが回帰だと思います。
回帰とは、簡単にいえば「数値を予測すること」です。
統計学的に詳細にいうと、
「説明変数xによる目的変数yの変化を y=f(x) の関数にあてはめること」
です。
※ 参考 ： 回帰分析
よくある例でいうと、家の広さから売却価格を割り出したり、
最高気温からビールの売上を予測したりすることは回帰分析になります。
既存のデータを参考にある程度値を推測できるようにしておき、
目的の値を予測できようにするのが回帰分析です。
体重から身長を予想してみる
例題を使って回帰分析をやってみます。
↓のように、体重と身長のデータセットを用意します。
| 体重(kg) | 身長(cm) |
|---|---|
| 40 | 150 |
| 41 | 152 |
| 42 | 152 |
| 40 | 155 |
| 50 | 160 |
| 53 | 161 |
| 55 | 165 |
| 61 | 169 |
| 68 | 177 |
| 78 | 180 |
これを見やすくするため、一次関数のグラフにプロットしてみます。
ここで体重65kgのデータがあった場合、身長はどのくらいと予測するでしょうか？
なんとなく↓のような身長(172cmくらい?）と予想するかと思います。
頭の中では、プロットされた既存データを参考にして、多分このへんだろうと予測しました。
この「データから学習して予測した値を算出する」のが機械学習です。
実際にデータを学習させて予測させるには、↓のようにモデルとなる関数を導き出して適用します。
各データを通る関数の定義がわかれば、体重から身長が予測できるようになります。
↑では予測用関数をだいたいの想定で引いてみました。
この一次関数の定義を
とします。
※ x = 体重 , y = 身長
この関数のθ0とθ1にあう適切な値を見つければ、体重から身長を予測することができます。
後述する最小二乗法を使うことで、ちゃんと数学的に算出することが可能なのでやってみましょう。
最小二乗法
今回は回帰分析でも基本的な分析手法である、「最小二乗法」を使ってみます。
最小二乗法の数式は、モデル関数を f(x) とするとき
が最小となるように f(x) を求めることです。
※f(x)はさきほど一次関数として記述した式
↓の図でいうと、プロットされたy座標と、関数の直線のy座標（y - f(x)）の
二乗の和が最小になるようにθ0とθ1を決めればよいという意味です。
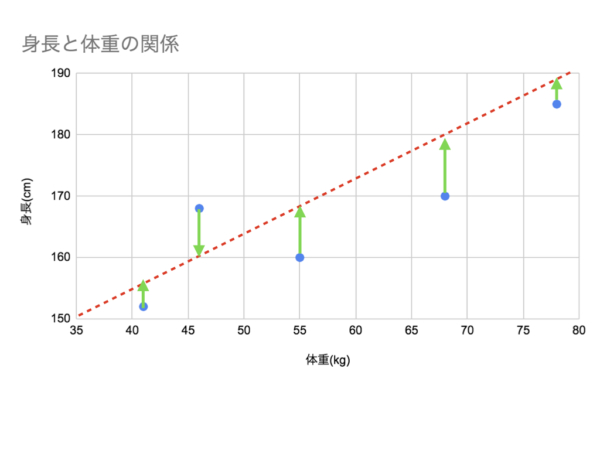
二乗している理由ですが、誤差に正と負の値がまざった場合に正しい値を出すためです。
絶対値でもいいかと思うかもしれませんが、
多くのmachine learningアルゴリズムでは勾配を計算するとき絶対値の微分が面倒になるため、
一般的に二乗を使います。
※詳しくはこのへん参照
では↓の３つのデータを使って式に当てはめてみましょう。
仮にθ0を2、θ1を1と仮定して確認してみます。
| 体重x | 身長y | θ0=2 , θ1=1 と仮定したときのf(x) |
|---|---|---|
| 42 | 152 | 85 |
| 55 | 165 | 111 |
| 78 | 180 | 157 |
計算すると、
((152 - 85)^2) + ((165 - 111)^2) + ((180 - 157)^2) = 7934
となります。
この7934という値が小さくなるようにθの値を設定すれば、
体重から身長を予測する適切な関数になります。
プログラムで最小二乗法
ではプログラムで最小二乗法を使ってみましょう。
今回はscikit-learnを使って試してみます。
setup
pipでscikit-learnをインストールします。
% pip install scikit-learn
サンプル実装
↓のように、scikit-learnで最小二乗法をつかったサンプルを作成します。(least-squares.py)
# 最小二乗法モデルを使う
from sklearn.linear_model import LinearRegression
#x=体重データ y=身長データ
x = [[40],[41],[42],[40],[50],[53],[55],[61],[68],[78]]
y = [150,152,152,155,160,161,165,169,177,180]
model = LinearRegression()
# 学習開始
model.fit(x, y)
print('θ0:', model.intercept_)
print('θ1:', model.coef_)
# 65kgの場合の身長を予測
source = [[65]]
predicted = model.predict(source)
print('予測結果:')
print('x(体重):', source)
print('y(身長):', predicted)
LinearRegressionは最小二乗法の線形回帰です。
実行してみると、θパラメータが設定され、体重65kgの場合に予測した結果の身長が表示されます。
% python least-squares.py θ0: 119.98012552301255 θ1: [0.7977249] 予測結果: x(体重): [[65]] y(身長): [171.83224372]
まとめ
今回は回帰分析や最小二乗法について簡単に解説し、
scikit-learnをつかって最小二乗法を使った予測も試してみました。
次は最急降下法について解説する予定です。
